Phases in a soil element
The volume relationships commonly used for the three phases in a soil element are void, porosity,
and degree of saturation.
Void ratio (e) is defined as the ratio of the volume of voids to the
volume of solids.
$$e=\frac{V_v}{V_s}$$
Porosity (n) is defined as the ratio of the volume of voids to the total volume.
$$n=\frac{V_v}{V}$$
The degree of saturation (\(S_r\)) is defined as the ratio of the volume of water to the volume of voids.
$$S_r=\frac{V_w}{V_v}$$
It is commonly expressed as a percentage.
The void ratio and the porosity are inter-related as follows:
$$e=\frac{n}{1-n}$$
$$n=\frac{e}{1+e}$$
The specific volume (v) is the total volume of soil which contains unit volume of solids, i.e.:
$$v=1+e$$
The specific gravity of the soil particles is given by:
$$G_s=\frac{M_s}{V_s \rho_w} = \frac{\rho_s}{\rho_w}$$
The degree of saturation can e expressed as
$$S_r=\frac{\omega G_s}{e}$$
When a soil is fully saturated, \(S_r\)=1,hence:
$$e=\omega G_s$$
The bulk density ( \(\rho\) ) of a soil can be expressed as
$$\rho = \frac{G_s (1 + \omega)}{1+e}\rho_w$$
The saturated density ( \(\rho_{sat}\) ) of a soil can be expressed as
$$\rho_{sat} = \frac{G_s + e}{1+e}\rho_w$$
The dry density ( \(\rho_{d}\) ) of a soil can be expressed as
$$\rho_{d} = \frac{G_s}{1+e}\rho_w$$
The bulk unit weight ( \(\gamma\) ) of a soil can be expressed as
$$\gamma = \frac{G_s (1 + \omega)}{1+e}\gamma_w$$
The buoyant unit weight( \(\gamma '\) ) of a soil can be expressed as
$$\gamma ' = \frac{G_s -1}{1+e}\gamma_w$$
The dry unit weight ( \(\gamma_{d}\) ) of a soil can be expressed as
$$\gamma_{d} = \frac{G_s}{1+e}\gamma_w = \frac{\gamma}{1+w}$$
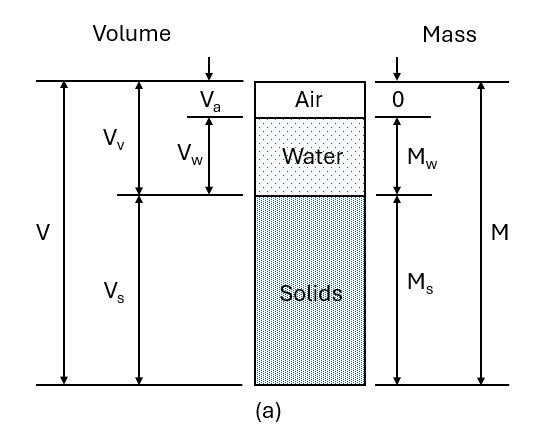
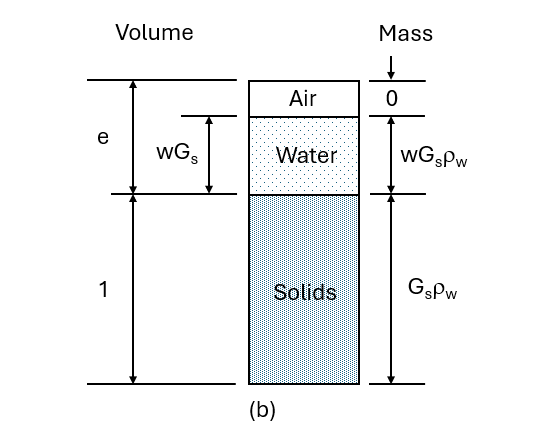
Figure 1 - Phase diagrams
